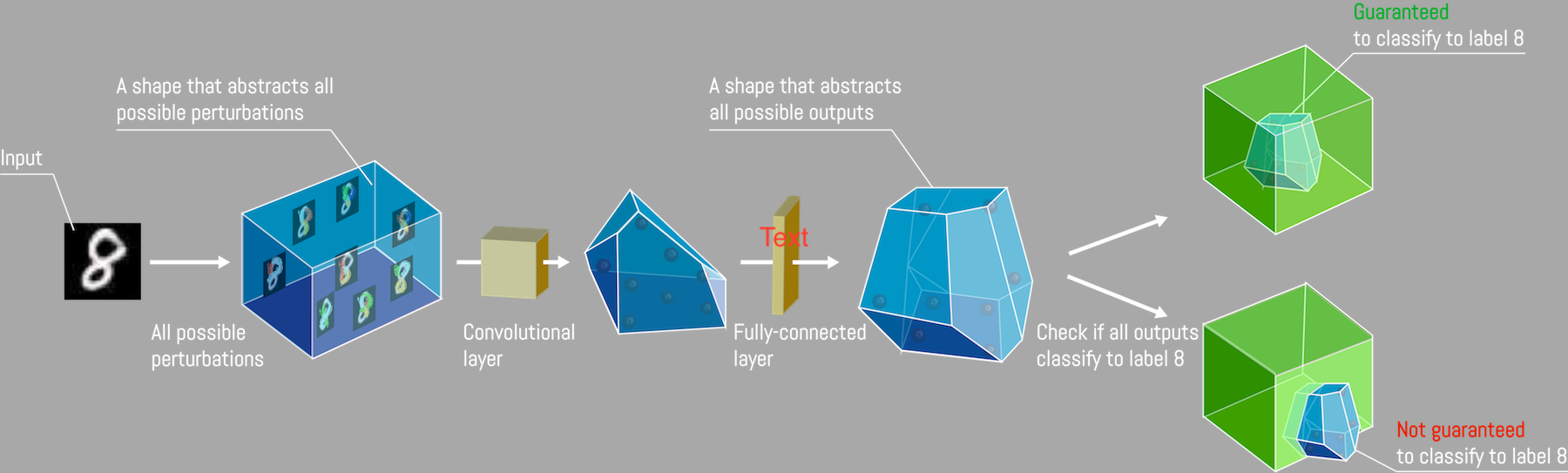Image credit: safeai.ethz.ch

Introduction

This is a review of the course "Reliable and Trustworthy AI", from ETH Zurich.

The course can be found here. To their great credit, all course materials except the very last lecture and the project information are available for free online.

My motivation for following this course was to learn about robustness. I think robustness occupies an interesting space, like interpretability, both of interest to mainstream academia & industry, and also of interest to people concerned about existential AI risk. I also have an aesthetic appreciation for the practical role of proof in robustness research.

Adversarial Robustness

In Machine Learning, we say a system is robust if its behaviour doesn't change when its circumstances change. More concretely, a robust system that has been trained on some data to perform a task will continue to perform that same task even on inputs that are out-of-distribution with respect to the training data.

This is a desirable property, both for the short-term and the long-term. In the short term, robustness failures are often exposed via adversarial attacks. An adversarial attack proceeds as follows: take some input that a model performs well on (correctly classifies as a dog, say). Then, add some carefully constructed random noise to the input, often of small enough magnitude that the resulting input is more-or-less imperceptibly different to the original. Finally, run this new adversarial example through the model, and observe that the model performs shockingly poorly.

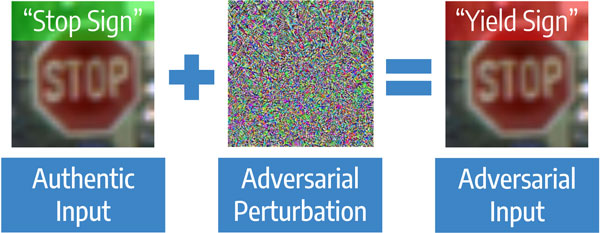
Image credit: ercim.eu

The course focuses in on adversarial robustness (robustness to these adversarial attacks). It's very well taught: Prof. Vechev takes his time to explain new concepts carefully, and there are several worked examples. Often painstakingly worked.

There are 3 main angles in the course:

1. Finding adversarial examples (demonstrating robustness failure)
2. Proving the absence of adversarial examples (certifying robustness)
3. Training models to be resistant to adversarial examples (adversarial training)

First, we get the lowdown on various algorithms for performing these attacks. The simplest to understand is Projected Gradient Descent (PGD). Suppose we want to find an adversarial example which misclassifies a cat as a baboon. PGD would work as follows:

1. Iteratively perform gradient descent on an image of a cat $I_0$, where the "loss" function is the activation of the "baboon" output neuron minus the activation of the "cat" output neuron. After the $n$-th iteration we have $I_n$.
2. As soon as the distance between the $I_n$ and the $I_0$ exceeds some $\epsilon$, project $I_n$ onto the $\epsilon$-ball surrounding $I_0$.

The first step tries to find an image that is classified as a baboon. Then the second step ensures that this image is sufficiently close to the original cat image that this counts as a mis-classification.

Despite being quite crude, PGD actually works pretty well in many cases, according to the lectures.

One thought I had while learning these techniques is that there seems to be an underlying assumption that, for any image with correct classification $c$, perturbing that image slightly should not change the classification. This assumption is clearly too strong, because it implies that every input should be classified the same (by repeatedly perturbing, any image could be perturbed into any other).

There's some good intuition behind that assumption. The key thing to understand is that we don't care about all inputs equally - in reality, we only care about stuff we might actually encounter. As discussed in the lectures, a better approach is to talk about the adversarial accuracy of the network as a kind of combined measure of both accuracy and robustness. The adversarial accuracy (with respect to some distance metric $d$ and some size $\epsilon$) refers to the probability that an input drawn from the data's distribution would be robustly classified correctly, i.e. it and any perturbation of it of magnitude $< \epsilon$ would be correctly classified. The assumption of the above paragraph can then be revised as follows: a good model should have high adversarial accuracy.

OK, so we have a notion of "how robust" a network is. Much of the remainder of the course is about how to compute the adversarial accuracy in a way that is provable.

Certifying Robustness

In order to calculate adversarial accuracy, we need a way to figure out whether there exists any adversarial attack on a particular input. Much of the course focuses on finding certifiable (i.e. provable) methods for demonstrating the absence of such an attack.

Most of these techniques are similar: first, we draw a ball around our input point. Then, we approximate this ball with some kind of $n$-dimensional polygon (called a "relaxation"), such that the polygon is a superset of the input ball. We can then "push" this relaxation through the network, taking approximations where computationally convenient, as long as we only over-approximate and never under-approximate. Finally, we can use linear programming techniques to figure out whether the resulting relaxation is correctly classified.

These techniques are fascinating, and incredibly clever! There are various different ways to constrain the polygon, with different accuracy and computational tradeoffs, such as Zonotope and DeepPoly.

By focusing on provability, the final result (robustness of a given point) is independent of any particular method for finding adversarial examples.

For each technique to certify the robustness of a point, there is a dual technique for adversarially training a network. This works roughly by replacing the regular loss function of gradient descent with the maximum loss achievable within the input point's ball, calculated using relaxation techniques above (which are conveniently differentiable).

Robustness-Accuracy Tradeoff

I think this work is really valuable, especially since adversarial training does actually produce networks that can be certified robust. However, it's important to note that, when training adversarially, the ordinary accuracy drops significantly.

To me, this makes sense. Adversarial training feels like it shouldn't make the network more robust without impacting accuracy. The reason is the fact that these adversarial examples exist and are so easy-to-find and pervasive in the first place! Especially given how well deep learning systems perform both in training and in the real world. It seems to me that the easiest thing for gradient descent to find is a network that is highly susceptible to adversarial attacks, so we're making its task strictly harder.

I think that expecting adversarial training to work just as well as ordinary training suggests a certain hypothesis about adversarial examples, namely that they're not necessary to the task-relevant parts of the network. In other words, if we use adversarial training and expect to get similar results as non-adversarial training, we implicitly believe that the out-of-distribution inputs just happen to be completely off-base. The alternative is that these adversarial examples are in fact necessary to get such good performance in-distribution; that the activation landscape in out-of-distribution spots has to look crazy in order to massage the in-distribution activation landscape into something reasonable. If this is so, then adversarial training is just going to push the craziness into parts of the landscape that we haven't yet figured out how to access reliably. I'm not saying I believe this, I'm just saying it seems plausible.

Robustness and Interpretability

One of my favourite parts of the course was the lecture on interpretability, and its links to adversarial robustness. The lecture covered some interpretability basics, including the idea that we can understand a particular neuron in a network by finding an input which maximises that neuron's activation function. We find this image by running gradient descent over the input, which is an interesting parallel between this interpretability technique and finding adversarial examples.

To me it makes sense that the two sub-fields are linked. The existence of adversarial examples means a network is not computing the function I would imagine it to be computing; adversarial examples illustrate a gap between how the model sees the task and how the humans see the task. Interpretability also aims to bridge that gap, by giving us direct insight into how the model works.

Something I didn't personally know is that these pretty images are the result of very aggressively regularizing. Similarly good results can be found on networks that were trained to be provably robust, but without the aggressive regularizing. What exactly does this mean? One provocative answer would be that networks trained to be robust are also just naturally more interpretable.

Considering the doubts I have about how robustness training works at the moment, this makes me very optimistic about the future of the interplay between these sub-fields.

How relevant is robustness to AI Existential Risk?

I plan to write more fully about this in the future. There are obviously lots of short-term risks associated with these adversarial examples. Some particularly worrying adversarial attacks involve "real life perturbations", e.g. putting bits of tape on a stop sign to fool a self-driving car's computer vision system into thinking it's a 100km/h sign.

There are also slightly less obvious longer-term risks. It's very easy to find these adversarial attacks, which (to me) suggests these attacks are just the tip of the iceberg of behaviour it's possible to tease out of a model with the right, carefully-crafted inputs.

Having said that, all adversarial attacks considered in this course are constructed deliberately rather than found "in the wild". That suggests the threat model is humans corrupting an ML system, or perhaps advanced ML systems corrupting other ML systems. To me this means robustness falls outside the field of alignment research, but only barely.

Conclusion

I really enjoyed this course! I'd like to attempt a capstone project where I code up a certifier, and an adversarial trainer.

I'd also like to read more broadly about robustness. Perhaps there are kinds of robustness that are more relevant to long-term considerations?